In this blogpost, I will attempt to find an approximation for the series posted in part 2. In part #2, we had the table:
Table 2. The table displays the X number of investments that are accruing value over an infinite J period. In our model, we had X = J hence setting J to infinity is an obvious over approximation. The shape produced by the cells is rectangular (J x X) where as in the true model it is triangular ~1/2(J x X).
Let’s change the definitions slightly and make the rectangular array into a square. Additionally, let’s also change the definition of each variable such that J = # of periods that accrue ROI and X = #investments + 1. For example, if we have 3 investments during 4 periods, then we have J = X where (J,X) is (4,4) array:
| ROI based upon the period we invested in (1/r) | Partial Sum of each investment | ||||
| Period 1 ROI | Period 2 ROI | Period 3 ROI | Period 4 ROI | A1[1-rn]/[1-r] | |
| Investment #1 | $1/2 | $1/4 | $1/8 | $1/16 | ½[(1-1/2)4]/(1-1/2) |
| Investment #2 | $1/3 | $1/9 | $1/27 | $1/81 | 1/3[1-(1/3)4]/(1-1/3) |
| Investment #3 | $1/4 | $1/16 | $1/64 | $1/256 | 1/4[1-(1/3)4]/(1-1/4) |
And so we can generalize the sum of each investment for all ROIs in the right hand column solutions as:
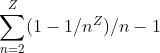
It isn’t clear to me how to mathematically dissect this series. One attempt is to represent it as an underapproximate in integral form:
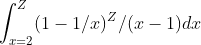
Using our example case of Z = 4, this factors nicely by partial fractions to:

Where we can evaluate each individual giving us the indefinite form of:
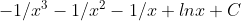
We choose to use a Z = 4 as we have 3 investments for four periods of interest. Hence we need to calculate this through [4,2]. Expanding this out we have:

The above evaluation only works for Z = 4. If we had more ROI periods we could also have more investments and hence more terms to integrate. So we can try to generalize (#4).
We want to be able to write out the above integral type in a way that can be evaluated even when there’s 49 investments over 50 ROI periods. It wouldn’t make sense to hand write the 49 polynomials and 1 logarithm for the lower and upper bounds. So we can try to generalize the pattern for [2,Z] as:
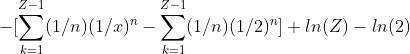
So
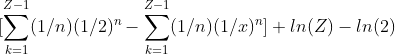
Final Thoughts: The last two equations are remarkably similar to the partial sum of a power series. As interesting as that might be, it isn’t obvious how to solve this further. I tried using, yet not even Wolfram alpha intuition on how to solve even one of the series. Even if I did have the “aha” moment it is still all a step in the backwards direction. The approximation made via our integral (Eq 2) produced a sum that evaluates to roughly $0.85 (Eq 5) whereas the actual sum should be $1.76. Finding a closed form of (Eq 1) directly instead of using an approximation might actual be more time efficient than any trying to find other approximations. If anyone better at math knows how to solve this, feel free to leave the solution in the comment section. I’d greatly appreciate it. If not, I appreciate you reading this far such a technical post.
Thanks,
Ben
