*This is just a continuation of the first blogpost titled “Modeling a Risk-Averse Investor in the Stock Market Pt. 2”. *
Finding an Upper Bound for our Heuristic:
To approximate the upper bound, let’s take J –> ∞ and not include the investment# 1 case as it is a special case then we have:
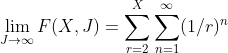
Above, we shifted the index of r by 1. It now has to have an initial value of r = 2 insuring the first-rate equals ½.
We can make another table to intuitively understand what this represents:
| ROI based upon the period we invested in (1/r) | Sum of each investment | |||||
| Period 1 ROI | Period 2 ROI | Period 3 ROI | Period 4 ROI | Period J | ||
| *SPECIAL CASE* | $1/1 | $1/1 | $1/1 | $1/1 | + … | 1+1+1+1 + … = $J |
| Investment #1 | $1/2 | $1/4 | $1/8 | $1/16 | + … | ½ + ¼ + 1/8 + 1/16 + … = $2.00 |
| Investment #2 | $1/3 | $1/9 | $1/27 | $1/81 | + … | $1/3 + $1/9 + $1/27 + …= $3/2 |
| Investment #3 | $1/4 | $1/16 | $1/64 | $1/256 | + … | $1/4 = $4/3 |
| Total sum of all investments ~$4.33 + $J |
Table 2. The table displays the X number of investments that are accruing value over an infinite J period. In our model, we had X = J hence setting J to infinity is an obvious over approximation. The shape produced by the cells is rectangular (J x X) where as in the true model it is triangular ~1/2(J x X).
So, we can clearly see that:
Investment #1 produces –> $J
Investment #2 produces –> $2/1
Investment $3 produces –> $3/2
Investment $4 produces –> $4/3
By induction, we can see the pattern for the sum of each investment # — barring the first investment — follows a nice pattern. Let’s remove the investment and shift the index of the investments by one hence.
Special case #0 produces –> $J
Investment #1 produces –> $2/1
Investment #2 produces –> $3/2
Investment $3 produces –> $4/3
Investment $4 produces –> $5/4
Hence for some large number of investments J we find:
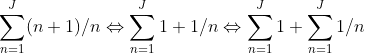
From literature, we can conclude that this approximates to
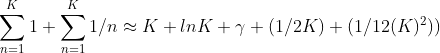
Hence going back to our original function F(X, J) to find the sum of the investment we get:
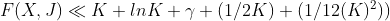
Finding the lower bound:
I’ll make this inaccurate but simple. We will just say that K is the partial sum of the harmonic series. If you reference the tables this is obviously true. The series representation of the diagonal starting at cell (1,1) going to cell (X, J) hence the lower bound is:
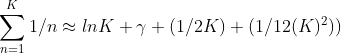
Relevance in real life:
This model more accurately represents real life initial investment is not a mere $0.50. We can just solve this problem by multiplying our initial investment value by some constant A to get a large initial investment. This is the same as writing for the upper bound:
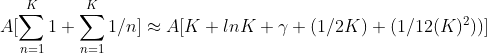
Or the lower bound:
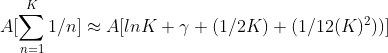
Let’s say that A = 10,000 and the investing period goes for 10 years.,

We will have for the initial investment $0.50 * 10,000 = $5000. We can expect our return to be roughly bounded by: ($2.93)*10,000 < value of portfolio < ($12.93)*10,000
$29,300 < value of portfolio < $129,300
The lower bound is obviously grossly wrong and hence the minimum should be higher. Regarding the maximum return, it seems feasible that a conservative investment would yield a YOY return would of 38.4%. Even though this maximum boundary seems high relative to the standard 10-12% expected YOY, it isn’t unheard of. There are at least 100 ETFs — many of whom are publicly traded.
If we wanted a more realistic answer, then we need to include more parameters. We could either or both of the following fixes:
- Find a more accurate lower bound approximation and/or find the closed form solution.
- Multiple the series by (-1)^n giving us oscillations. This would represent volatility in that occurs in actual markets.
An example #2 would be:
Year 1: +$0.50
Year 2: $-0.25 + $0.33
Year 3: +$.125 – $0.11 + $0.25
Etc, etc.
Another interesting question would be what if the investments were sporadic. This could be model explicitly to have the stocks only bought in prime year investing 1/prime dollars per stock (i.e. 2, 3, 5, 7, 11 for a $1/2, $1/3, $1/5, $1/7, $11, respectively). You even theoretically add the cherry on top and have force model include oscillating too. This heuristic would be the most accurate yet the most hard to calculate – way out of the scope of this blog.
If you read this far, I congratulate you. If you read this far and understood what was said, give yourself a pat on the back and a round of applause at same exact time (it’s impossible to do that) for being a diligent reader. I will post a part III if I can provide a closed form solution to the equation at the top of this page, or present more economic relevance of the model.
~Ben
