The infamous British TV game show starring two contestants who would interact with one another to either split or steal a cash prize. It’s a prime example of the classic game of Prisoner’s Dilemma. Prisoner’s Dilemma is a game where two contestants can either work together to share an outcome or betray one another in hopes of getting the entire prize. The catch is that if they both betray one another, then they both get the worst possible outcome.
The game’s contestants go through multiple rounds, each with an increasing cash prize. In each round they have a few minutes to talk to one another to try and convince the other participant to lean one way or another (either split or steal). The few minutes the contestants have are a prime example of cheap talk. Cheap talk is where people can share information, but it does not negatively impact them in any way. This could lead to lying, cheating, and manipulation to get others to do what you want. As a contestant on the show, you never know if the other person is lying and trying to manipulate you or if they are truthful.
I have modeled an example of what happened in this game
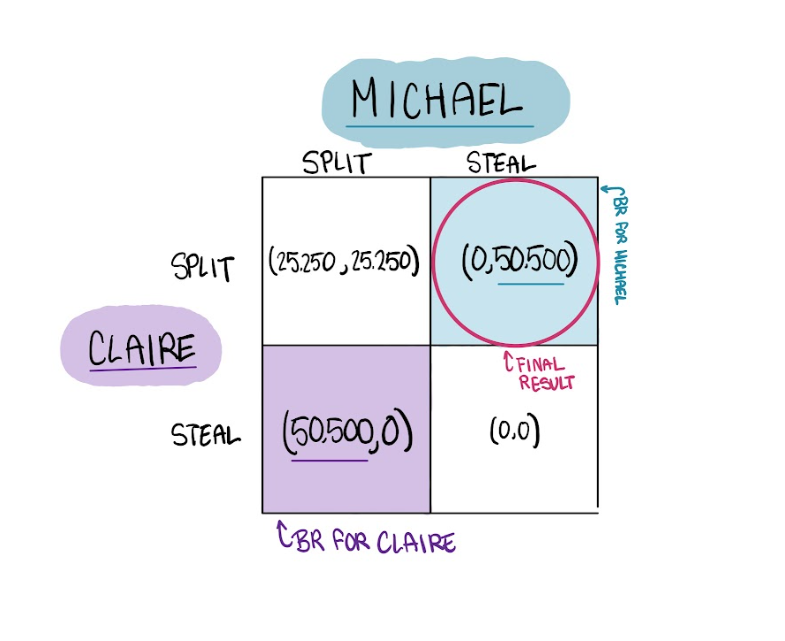
Michael and Claire have the ability to either split or steal $50,500. During the cheap talk phase, Michael convinced Claire to split the money with him. Claire trusted him and decided to split. When the golden balls were revealed, Michael ended up betraying Claire’s trust. He stole the money and took the whole $50,500 home and Claire gets nothing.
This is a good example of a Prisoner’s Dilemma because there are two Nash Equilibriums (two naturally occurring end results). Each player has a best response to steal when the other splits (50,500 > 25,250). However, this leads to a dilemma because if both players act according to their best responses, they both get nothing. That’s why Michael tried to manipulate and cheap talk Claire into splitting. This worked out for Michael in the end, and he went home $50,500 richer.
