Last Thursday students at the University of Puget Sound band together to boycott Magoo’s due to the increase in price of their beer pitchers from $5 to $6.50. Dirty Oscar’s Annex instead proved to be the popular choice of the night and experienced an increase in customers. While the majority found themselves in the famous tater tot bar that is DOA, few were left out of the memo or stuck to their preferences and brought their business to Magoo’s. Now that this Thursday has rolled around, loggers are left confused of where to go tonight. Previously posted this week on the “Boycott Magoos” Facebook page a student asked, “Yo where we going this Thursday?” Just today another post was made that had poll asking where students were headed out to tonight. Why they asked Facebook and didn’t make the decision on their own points us to see this dilemma as a coordination game.
In coordination games, players are the happiest when they make the same decision as the other players. This makes sense in the context of students choosing which bar to go to, since students want to be able to socialize with classmates and need to be together to do so. While overall all players are happiest when together, both groups can have preferences over where it is that they are together at. This is modeled in the game matrix below.
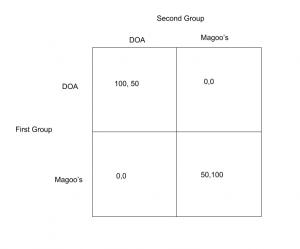
In this model there are two groups of students, and both groups have the same choices, they can either attend DOA or Magoo’s. The first quadrant then shows us what happens when both groups pick DOA, the second quadrant if the the first group picks DOA and the second Magoo’s, the third if the first group picks Magoo’s and the second DOA, and the fourth quadrant if both groups pick Magoo’s. Inside each quadrant are the payoffs each group receives based off of the choices they have made. If both groups pick DOA, then the first group is very happy with a payoff of 100 to represent that. The second group is also happy with a payoff of 50, but not as happy because their preference is for Magoo’s. So, if both groups pick Magoo’s, the second group is really happy with a payoff of 100, and the second group is still happy with a payoff of 50. If these groups end up in separate locations though both are unhappy, represented with payoffs of zero. While one group may prefer DOA to Magoo’s they would rather be at Magoo’s if that is where everyone else is going.
This matrix shows the importance of both groups coordinating, in order that they both end up in the same place so they can maximize their happiness. Tonight University of Puget Sound students are faced with this problem when deciding where to go out to tonight. Through social media and word of mouth, both groups will try to signal to each other, in hopes that everyone ends up at the same bar. So will the loggers figure it out and maximize their happiness and end up at the same bar? And if so, will that bar be DOA or Magoo’s? We will find out tonight. Happy Thursday!