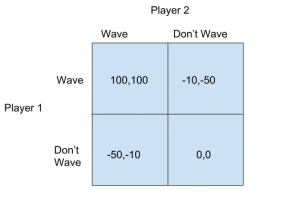
We have all been in a situation where we are unsure if we should wave at an acquaintance we see or to continue on with ourselves without waving. Whether this happens in the grocery store, on the street, or walking around your college campus it is all equally awkward and uncomfortable. There is that one moment, after you both make eye contact, that you must decide if you will send them a salutation or withhold. While we have all faced this we probably have not thought of this scenario through an economic lens, but we can use a game matrix to weigh the payoffs of to wave or not to wave. We will assume this is a static game; that is, both players have to make a simultaneous decision to wave or not without information of the other’s choice. While these might seem partially unrealistic as you can sometimes throw in a quick nod after someone has waved at you, there are many scenarios where you only have a single moment in passing to make a decision.
We will create this matrix so that if both of you wave, you both gain the most utility, this is shown with the payoffs of 100 for each player, this payoff includes that happiness you get from enjoying a social connection with another human. If both players don’t wave then the situation remains neutral with a payoff of zero for each. If one player waves and the other-other player does not though, then both players get negative payoffs. I assigned the player who doesn’t wave to have more negative feelings from this interaction with -50, than the player that waves but does not get a wave back with a payoff of -10. These payoffs, however, would depend on an individual’s tastes and preferences. Personally, I feel more guilty and mean if I do not wave back than I do embarrassed for sending an unreturned wave.
Using this game matrix we then can decide if we should wave or not to the passing acquaintance based off of our beliefs of what they will do. If we believe they will wave every time as they are an extra friendly person, then the optimal choice would be to wave as well. If the belief is that they will never wave, then the optimal choice is not to wave just like them. When we believe they are just as likely to wave as not to wave though, the best decision to make is to wave. Using this game matrix for when our belief is 50/50, waving has an expected payoff of 45 while not waving has an expected payoff of -25. This reaffirms what Mari Gayatri Stein once said, “Better to be the one who smiled than the one who didn’t smile back.” So while it may just seem like a cheesy quote, we have the economics to back that statement up.