So three weeks ago, I spoke with Ian Hughes about his thesis, titled:
Identifying Socioeconomic Indicators of College Attendance with Classification Trees
Much of Ian’s research centered around intergenerational income mobility and barriers to it. Some of the research showed that “low-income students are subject to less college preparation and lower test scores because of their financial situations”, which contributes to more difficulty in using education as a route out of poverty.
Much of the literature surrounding wealth, race, and parental education in connection with children’s college attendance is well established, so Ian included some other characteristics that have not received as much attention. For his data set, Ian examined the Panel Study of Income Dynamics (PSID) from the University of Michigan. It covers household employment, income, wealth, expenditures, health, child development, education, and numerous other topics.Some of the more atypical variables Ian investigated included: the overall positivity of the child, their emotional well-being, and their impression of their school’s safety.
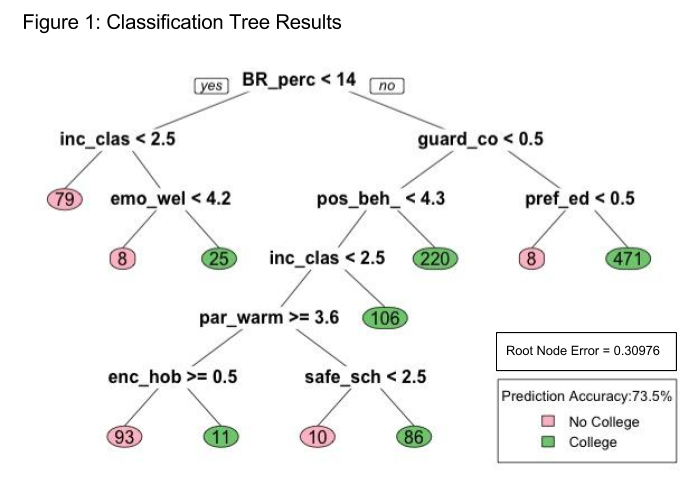
In order to tackle this problem, Ian developed both an OLS binary response regression and a classification tree machine learning approach. He focused on the classification tree, a technique borrowed from data science, which essentially evaluates the predictive capacity of explanatory variables, and eliminates those which are poor predictors. Below you can see the results.
Here you can see the descriptions of all the variables used, but the main ones to know are the binary response variable, college, and the Broad Reading percentage, which is used as a proxy for children’s intelligence. In this classification tree, it takes an imaginary child, then evaluates their likelihood of going to college. So it operates like a decision tree in game theory, but instead of strategically choosing a path, it shows what a child would do based on their characteristics. In my interview, I think Ian put it best, saying,
“[The classification tree] tells a different story…it’s more narrative-based compared to a regression where you have to build all these scenarios in order to tell the story…If you were given a sample child, you could predict whether or not they go to college a lot more easily than using a regression where you’re still given a percentage chance.”
Classification trees also perform another important function, by building nodes based on combinations of explanatory variables, they illuminate the relationships between the variables in a way that an OLS regression would not. For example, if neither of a child’s guardians completed 14 years of schooling, then a parent’s preference for a child receiving more education becomes critical to their odds of attending college.
As far as Ian’s conclusions go, it seems that the regression found parental income is still one of the most important factors in determining college attendance, but that other variables have significant impacts when paired together in relationships by a classification tree. Or as Ian put it,
“Combining the two distinct models helps answer the question, “which childhood environment factors explain college attendance?”, with more clarity.”
No matter how you evaluate it, effective studies are necessary if we are to tackle a problem as far reaching as intergenerational mobility,
-Max Coleman