If you’ve spent any time at UPS, you’ve probably thought at some point, “Is there actually going to be anything good at the SUB today, or should I go off-campus?” While the connection between economics and going to the SUB may not be clear, just remember that economics is the study of how people make choices.
I’m currently taking an Economics of Online Dating class (Econ 341), which has a large focus in economic model building. A couple weeks ago, we were asked to create a model of decision-making under risk. Risk is defined as a situation in which all possible outcomes and the probabilities of those outcomes are known. So, rolling a dice is risky, whereas trying to predict the weather involves uncertainty, or not knowing all the outcomes or their probabilities. When you go to the SUB, especially if you don’t check the menu online, there is a certain amount of risk that you won’t be overly pleased with your outcome. So, I decided to make a decision-making model for the SUB, and provided other options so there was an element of actual choice.
In order to make this model more manageable, I made certain assumptions:
- The decision maker has no dietary restrictions
- The decision maker is only concerned with their dinner entrée
- The decision maker’s proximity to the SUB or other locations isn’t considered
- The decision maker has a UPS meal plan
- The decision maker has sufficient funds to purchase alternatives with cash
- The decision maker could make food at home
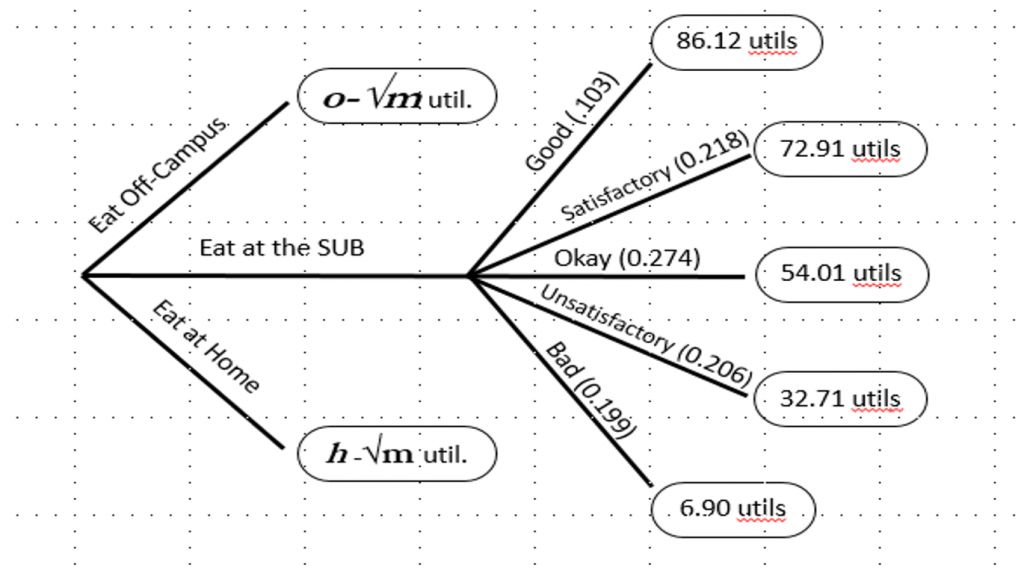
I realize that these assumptions aren’t true 100% of the time, but once a model becomes too complex, it loses some of its power to simply explain a problem. To gather information from this model, I needed two things: a measure of how people valued their options, and what their options were. For the first, I used the economic concept of utility, which is a measure of how people value outcomes. For the second, I looked at the menu for the dinner entrée at different stations in the SUB and charted it out for two weeks. I then asked 11 current students without dietary restrictions to give me utility values between 0 and 100 for their options.
I then sorted these values into five categories: good (81-100), satisfactory (61-80), okay (41-60), unsatisfactory (21-40), and bad (0-20). From the number of occurrences of values in these ranges, I worked out the probability of the outcomes averaged across the 11 students. I was also able to work out average values for each of the categories, and used this information to create a decision tree model. Decision trees use a concept called expected utility, which boils down to the weighted sum of utility values, weighted by probability. Essentially, economists expect decision-makers to act rationally to maximize their utility, and expected utility allows decision-makers to try and do that.
I’ve also included some parameters, or variables that have no specified value.
- h is your expected utility from making something at home, which could change with: how recently you bought groceries, if you have time, if you want to put in the effort, etc.
- o is your expected utility from eating out, which could change with: how much real money you have to spend, time, if other people are going, if other options are closed, etc.
- √mis your utility for money, in this case the money you would spend on eating off-campus or to buy groceries to make food at home.
This allows decision-makers to evaluate their expected utility from the SUB (47.67 utils) against other options which change with other circumstances, such as how much cash you have on hand, or how often you’ve eaten at the SUB. Finally, here’s some mathematical expressions which could help make these decisions for you!
- If 47.67 > h-√m, & 47.67 > o-√m, go to the SUB.
- If 47.67 > h-√m, & 47.67 < o-√m, eat off campus.
- If 47.67 < h-√m, & 47.67 > o-√m, eat at home.
- If h-√m = 47.67= o-√m, then you are indifferent.
So if you’re ever trying to decide on whether you should go to the SUB or not, just remember to maximize your expected utility and weigh your options.